前面的专栏我们介绍了Adapt Tuning、Soft Prompt Tuning等微调技术，本文让我们跟随着论文《LORA: LOW-RANK ADAPTATION OF LARGE LAN- GUAGE MODELS》，来看一下LoRA微调技术。

1.Abstract(摘要)

首先我们看一下论文摘要，快速理解论文的核心内容：

• 问题：LoRA也是解决全参数微调参数量过大、成本过高的问题。
• 解决方案：论文提出了LoRA微调技术，冻结预训练模型权重，在Transformer架构的每一层注入可训练的低秩矩阵。
• 实验效果：LoRA大幅减少了训练参数量，与使用Adam微调的GPT-3 175B相比，LoRA将训练参数数量减少了10000倍，GPU需求减少3倍。

2.Introduction(介绍)

• 问题：全参数微调成本过高，现有高效微调技术扩展了模型深度导致了推理延迟or减少了模型可用序列长度。

  • 全参微调的主要缺点是新模型包含的参数量与原始模型一样多，进而导致成本巨大。如：GPT-3拥有1750亿参数，全参微调成本巨大。
  • Houlsby、Rebuffi等专家提出的高效微调技术，增加了模型深度，也会导致推理延迟，也可能导致减少了模型可用序列长度。

• LoRA的核心思想：

  • 可以共享一个预训练模型，在其基础上构建许多用于不同任务的小LoRA模块。
  • LoRA模块用两个低秩矩阵A和B，替换原有的参数。利用低秩矩阵的数学特性，减少参数量。

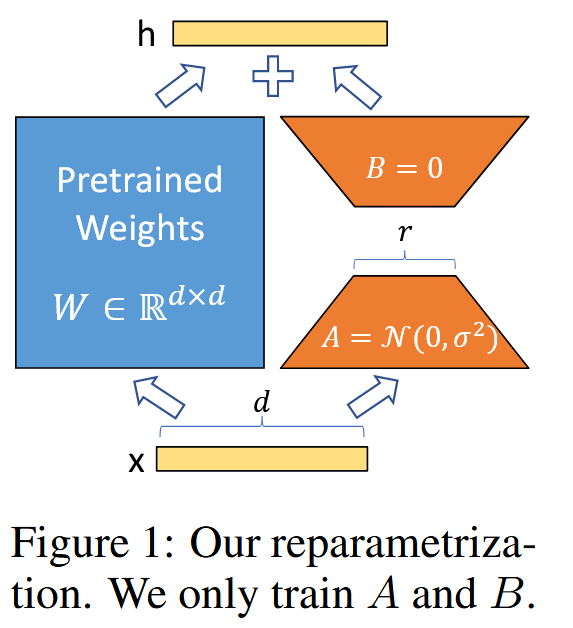
• LoRA的优势：
  • LoRA的这种设计使训练更加高效，将GPU计算量降低了3倍。
  • LoRA模块对Transformer的改变是线性的，因此不会由于加深网络结构导致推理延迟。
  • LoRA的设计和现有高效微调技术是正交的，可以和它们结合使用。

3.Design Decisions(实验设计)

(1)问题域

• 对全量微调建模：在全量微调下，预训练模型参数的初始值为Φ₀，随着梯度更新为Φ₀+∆Φ，则找到∆Φ的任务可定义为：

• 

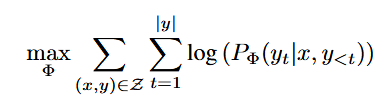
• 对全量微调缺点建模：∆Φ的维度等于|Φ₀|，当模型很大时，梯度更新Φ₀将导致巨大的计算成本。

(2)问题建模

LoRA是这样寻找突破口的：

• LoRA建模：∆Φ=∆Φ(Θ)，|Θ|维度«|Φ₀|，则找到∆Φ的任务可转换为对Θ的优化：
• 

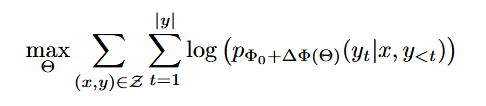
如何做到∆Φ=∆Φ(Θ)呢？其本质就是降维：

• 低秩矩阵：低秩矩阵的概念本文不会展开描述，小伙伴们可以复习一下线性代数。但低秩矩阵的本质是2个低阶矩阵的运算可以约等于1个高阶矩阵。
• 低秩矩阵与深度学习的结合：假设预训练模型的参数矩阵为W₀，则梯度更新可认为W₀+∆W。如果将∆W分解为2个低秩矩阵B和A，即W₀+∆W=W₀+BA_x。
• 低秩矩阵与Transformer的结合：在Transformer架构中，W_q、W_k、W_v，W_o分别表示Query、Key、Value、输出投影矩阵。W_q、W_k、W_v是单一维度为dmodel*dmodel的矩阵。W_q+∆W、W_k+∆W、W_v+∆W中的∆W分解为低秩矩阵B和A，则也将问题转换为∆W小矩阵问题。

4.Experiments(实验结果)

(1)实验结果

• 在GLUE基准测试中使用RoBERTa(基础和大型)和DeBERTa 1.5B获得了与全参数微调相当或更优的结果，同时只训练和存储了一小部分参数。

• 

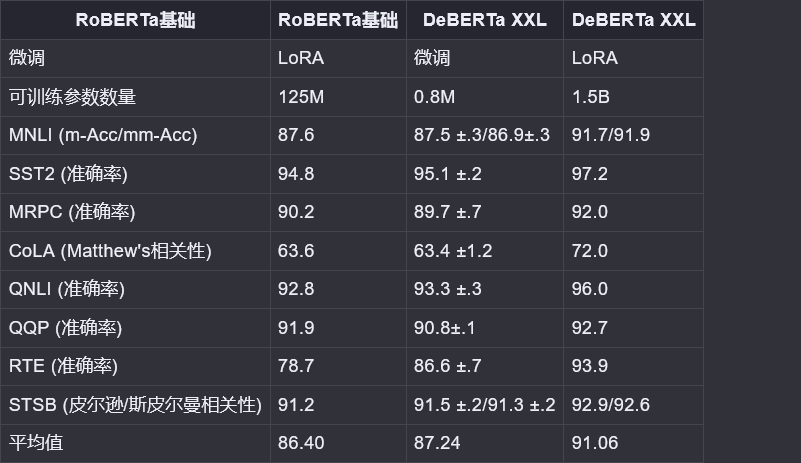
• 在GPT-2上，LoRA与全参数微调和其他高效调整方法和前缀调整相比具有优势。

• 

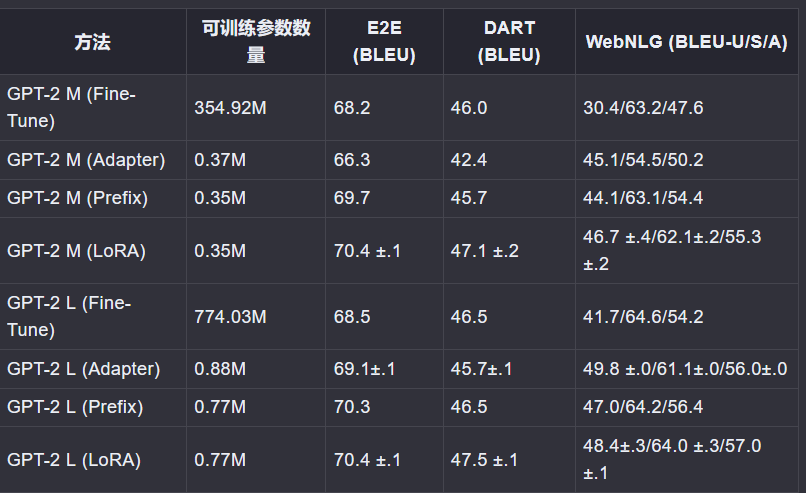
(2)关键发现

• LoRA与Transformer结合，应该如何划分低秩矩阵？

  • 实验证明：r=8或r=4时，适用于GPT-3(175B模型)的96层注意力层。
  • 实验证明：不要仅仅只刷新∆W_q或∆W_v，同时刷新它们会产生更好的性能。

• ∆W和W强相关，∆W增强了W学习到的一些特征。

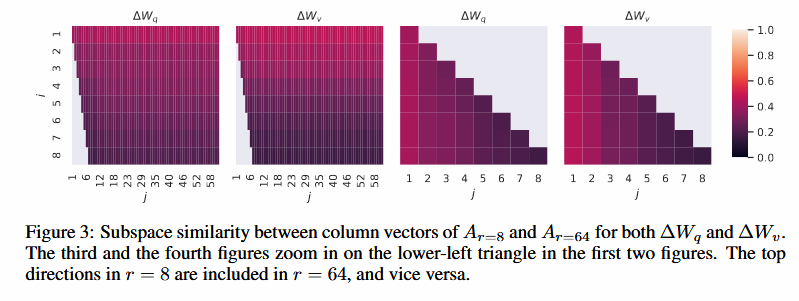
5.总结

从上述论文解读中，我们收获了如下技术观点：

• LoRA的核心思想：LoRA模块用两个低秩矩阵A和B，替换原有的参数。利用低秩矩阵的数学特性，减少参数量。。
• LoRA的优势：LoRA的这种设计使训练更加高效，且不会由于加深网络结构导致推理延迟。
• LoRA实验的关键发现：
  • LoRA与Transformer结合，要考虑如何划分低秩矩阵。
  • ∆W和W强相关，∆W增强了W学习到的一些特征。

论文链接：https://arxiv.org/abs/2106.09685