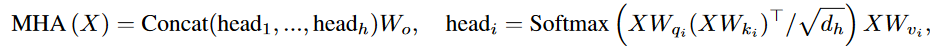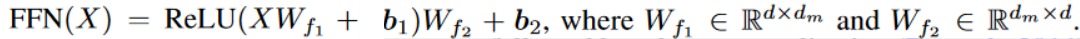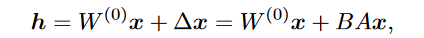今天我们通过解读论文《ADALORA: ADAPTIVE BUDGET ALLOCATION FOR PARAMETER-EFFICIENT FINE-TUNING》来学习一下AdaLoRA。

1.Abstract(摘要)

首先我们看一下论文摘要，快速理解论文的核心内容：

  • 问题：AdaLoRA也是解决全参数微调参数量过大、成本过高的问题。
  • 解决方案：论文提出了AdaLoRA微调技术，是对LoRA的一种改进，LoRA没有考虑不同权重参数的重要性不同。AdaLoRA以奇异值分解的形式参数化增量更新，有效地修剪不重要更新的奇异值，避免了密集的精确SVD计算。
  • 实验效果：在自然语言处理、问答和自然语言生成等多个预训练模型上的实验表明，AdaLoRA在低预算设置下，微调效果有显著的改进。

image-20240621144023004

2.Introduction(介绍)

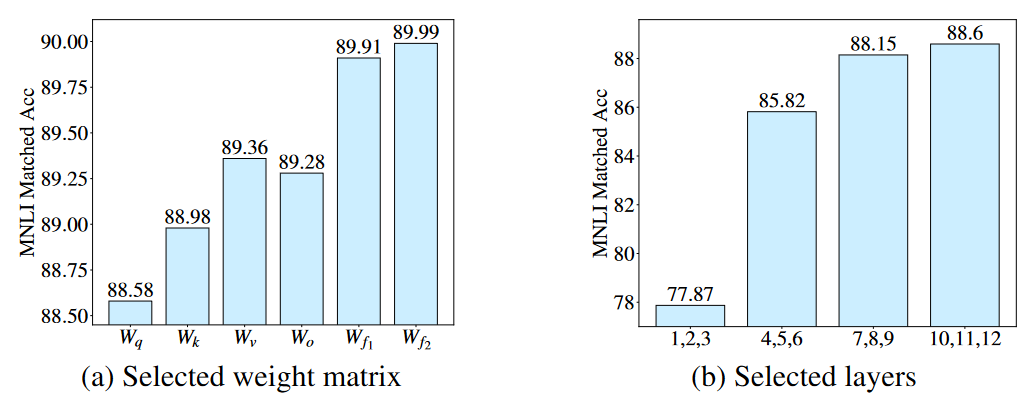
  • 问题：LoRA有哪些局限性呢？论文给出了一个测试。
    • 左图：针对不同模块进行LoRA微调，效果是不一样的。针对前馈网络FFN进行LoRA微调的效果要远优于自注意力模块的LoRA微调。
    • 右图：针对不同层进行LoRA微调，效果也是不一样的。10~12层的微调效果要远优于1~3层的微调效果。

image-20240621164711429

  • AdaLoRA的核心思想：

    • 通过上述实验可以看到：在理想状态下，微调关键模块/关键层的权重矩阵是最有效的，而微调不太重要的模块/层的权重矩阵不仅毫无意义，甚至有负面的影响。
    • AdaLoRA针对关键矩阵设置为高秩，对于不重要的矩阵修剪为低秩。设置为高秩的增量矩阵可以捕获更细粒度的特征。
    • AdaLoRA如何实现上述这种对秩的调整呢？答案是数学工具SVD(矩阵奇异值分解)，SVD是将高维矩阵拆分为三个矩阵，即∆=PΛQ。P和Q分别表示∆的左/右奇异向量，Λ表示∆的对角矩阵。SVD在数据科学、机器学习中应用广泛，常用于降维、数据压缩、噪声过滤、文本数据的潜在语义结构提取等。
    • AdaLoRA通过对某层、某模块的重要性评分，动态调整∆=PΛQ的秩。AdaLoRA构造了N个三元组，每个三元组Gi=(P, Λ, Q)，AdaLoRA设计了一种重要性度量方法，重要性得分高的三元组被赋予高秩。

  • AdaLoRA的实验效果：

    • 针对DeBERTaV3-base进行自然语言理解(GLUE)、问题(SQuADv1)进行了评估，AdaLoRA有了更好的性能表现。
    • 针对BART-large进行自然语言生成(XSum)进行了评估，AdaLoRA始终优于基线的性能。

3.Design Decisions(实验设计)

(1)问题域

  • 对Transformer的建模：Transformer模型有L个堆叠的块组成，每个块包含2个子模块——MHA(多头注意力)、FFN(全连接前馈网络)。

  • MHA函数：给定输入序列X∈Rn×d，MHA执行了h个多头注意力函数表示为

    • image-20240621184305094

  • FFN函数：前馈网络由两个线性变换组成，中间有一个ReLU激活函数。

    • image-20240621185258000

  • 对LoRA建模：LoRA的本质是用两个小矩阵替代一个大矩阵。

    • image-20240621185936493

  • LoRA模型的问题：

    • LoRA的低秩分解方法选择了相同的秩r
    • 不同层的矩阵参数都采用相同的AB分解方法吗？

(2)问题建模

  • SVD：SVD是对高维矩阵进行降维的行之有效的数学工具。
    • SVD的目标：将1个高维矩阵，转换为3个低维矩阵，并且可以通过调整秩r来控制对角矩阵Λ(公式3)。
    • Λ的数学性质：对角矩阵Λ的特征值逐步递减，不严谨地说特征值越高，这个维度的特征越重要。
    • Λ的近似：当我们用秩r舍弃对角矩阵Λ较小的特征值，就实现了降维的同时又不丢失有效的信息。
    • PQ的数学性质：在SVD中，PQ要满足正交性，因此论文中引入了对P和Q的正则损失约束(公式4)。
    • SVD的详细原理和数学推导本文不赘述，可以参考机器学习的PCA方法。

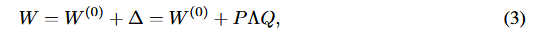
image-20240626162821750

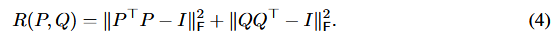
image-20240626170654390

  • 重要性评估：某一层的某个参数矩阵对于整个Transformer到底是不是重要的？

    • Gk,i： 假设G这个三元组表示训练过程中对P、Λ、Q的更新。
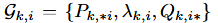
    • image-20240626170842830
    • C(P, E, Q)：假设C表示对P、Λ、Q的更新代价。
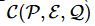
    • image-20240626171118350
    • R(Pk, Qk)：假设R表示P和Q满足公式4R(P, Q)正交性的代价。
    • L(P, E, Q)：则，L表示训练目标是要保证C和R都尽量小，才能得到满足训练效果的最优训练成本。
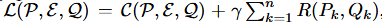
    • image-20240626171425594
    • Λ(t)k：则，Λ(t)k表示采用梯度更新的计算过程(公式5)。
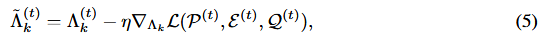
    • image-20240626171551548
    • 但是我们知道对每轮迭代、对每一层的高维参数矩阵进行SVD，存在巨大的计算成本，因此论文终于从逻辑上引出了重要性评估：
    • SVD剪枝：假设S是一个重要性评估的函数，那么Λ(t)k和S(t)k共同决定了Λ(t+1)k是否还有必要进行更新(公式6)。
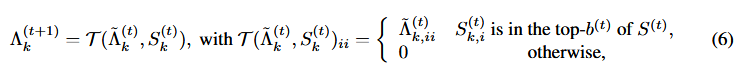
    • image-20240626171655605
    • Stk：重要性评估函数考虑P、Λ、Q三个矩阵重要性的影响(公式7)，其中**s(·)**表示具体的重要性计算方法。
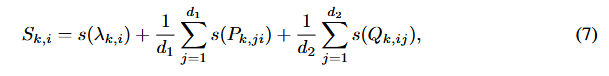
    • image-20240626172223409

  • s(·)的三种计算方法：

    • 不考虑P、Q的影响：对角矩阵Λ中特征值越大越重要，这是传统的SVD判定重要性的方法，这种方法忽略了P和Q对各层参数矩阵的重要性影响。
    • 考虑P、Q影响，但不考虑重要性函数的平滑：(公式8)。
    • image-20240626172632400
    • 考虑P、Q影响，但考虑重要性函数的平滑：什么情况会导致重要性不平滑呢？通俗地说，模型对于某一批次的数据已经训练地很好了，那么可能会导致认为当前的参数矩阵对整个模型并不重要。3个公式相当于增加了二级平滑的函数，保证了考虑P和Q的同时，也能相对客观地评估它们的重要性(公式9、公式10、公式11)。
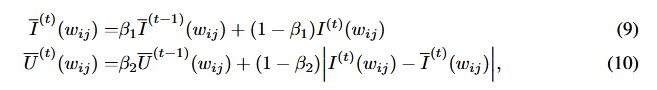
    • image-20240626172937743
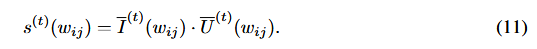
    • image-20240626172945391

4.Experiments(实验结果)

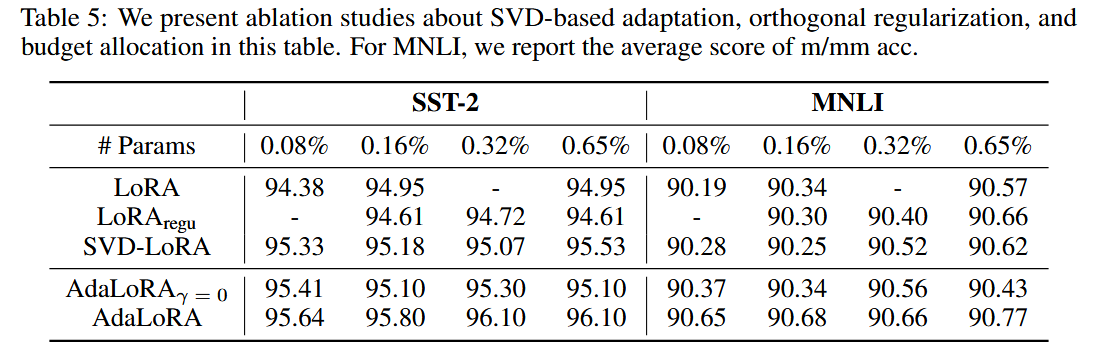
(1)实验结果

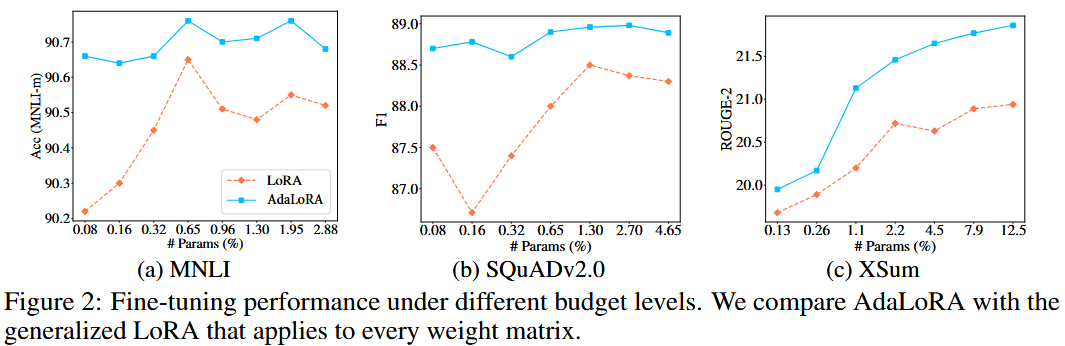
从整体的实验结果来看，AdaLoRA的微调效果全面优于LoRA。

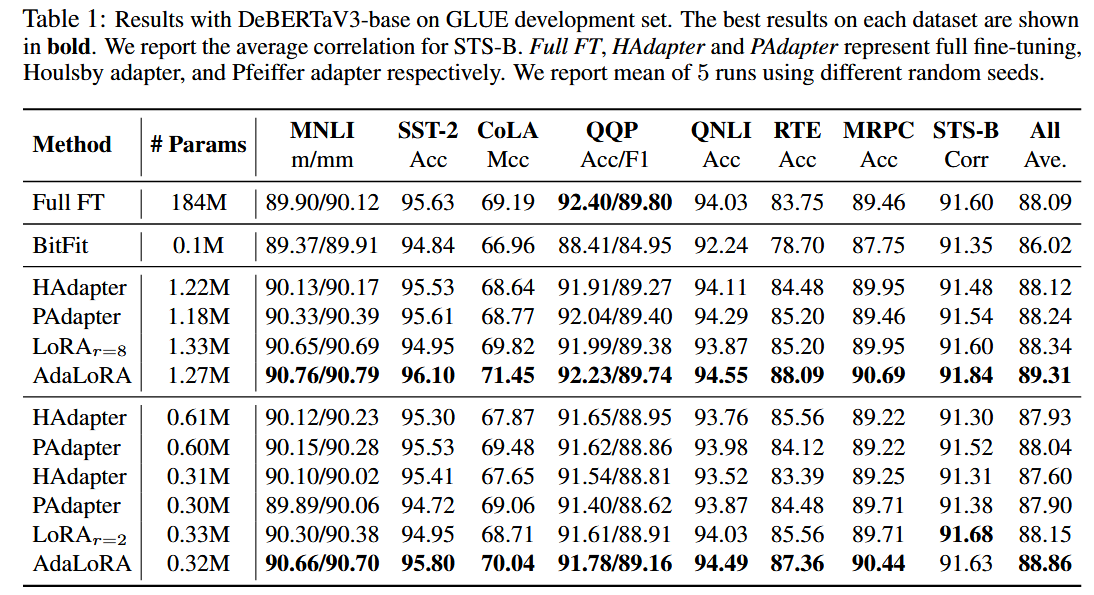
image-20240626174406600

(2)关键发现

  • 增加计算预算，AdaLoRA的训练效果会显著优于LoRA。

    • image-20240626173949733

  • SVD降维、保证PQ矩阵的正交性，对AdaLoRA的训练效果都有影响。

    • image-20240626174221946

  • Transformer中，FNN的参数矩阵重要性要大于自注意力层的参数矩阵、顶层的参数矩阵重要性大于低层的参数矩阵重要性。

    • image-20240626174532657

5.总结

从上述论文解读中，我们收获了如下技术观点：

  • AdaLoRA的核心思想：采用SVD、正则损失、二次平滑的重要性评估，精准地控制每一层的参数矩阵降维。
  • AdaLoRA的关键发现：
    • SVD降维、保证PQ矩阵的正交性，对AdaLoRA的训练效果都有影响。
    • Transformer中，FNN的参数矩阵重要性要大于自注意力层的参数矩阵、顶层的参数矩阵重要性大于低层的参数矩阵重要性。

阅读AdaLoRA最大的感触就是数学的奇妙，AdaLoRA是一个主要依赖数学公式推导解决算法问题的典型代表。

论文链接：https://arxiv.org/pdf/2303.10512